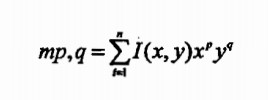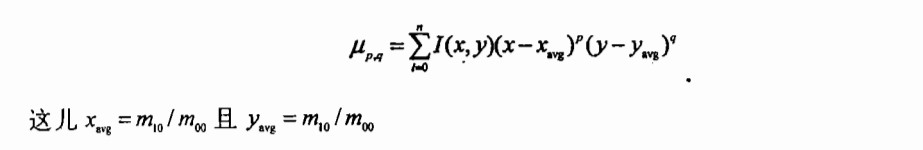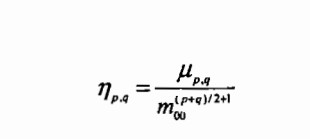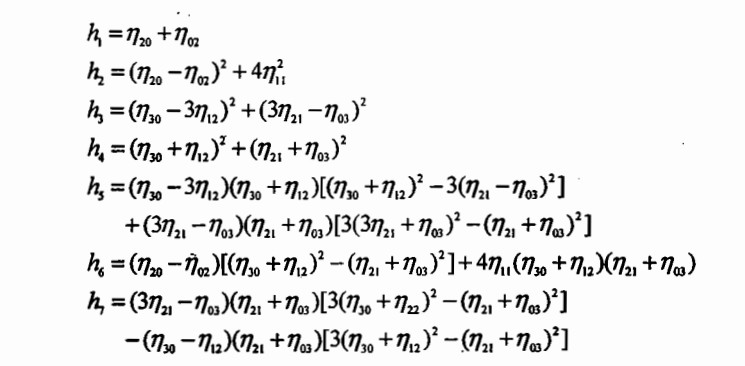一个跟轮廓相关的最常用到的功能是匹配两个轮廓.如果有两个轮廓,如何比较它们;或者如何比较一个轮廓和另一个抽象模板.

矩

比较两个轮廓最简洁的方式是比较他们的轮廓矩.这里先简短介绍一个矩的含义.简单的说,矩是通过对轮廓上所有点进行积分运算(或者认为是求和运算)而得到的一个粗略特征.通常,我们如下定义一个轮廓的(p,q)矩:

在公式中p对应x纬度上的矩,q对应y维度上的矩,q对应y维度上的矩,阶数表示对应的部分的指数.该计算是对轮廓边界上所有像素(数目为n)进行求和.如果p和q全为0,那么m00实际上对轮廓边界上点的数目.

下面的函数用于计算这些轮廓矩

void cvContoursMoments(CvSeq* contour,CvMoments* moments)

第一个参数是我们要处理的轮廓,第二个参数是指向一个结构,该结构用于保存生成的结果.CvMonments结构定义如下

[cpp]  

1. /* Spatial and central moments */    
2. typedef struct CvMoments    
3. {    
4.     double  m00, m10, m01, m20, m11, m02, m30, m21, m12, m03; /* spatial moments */    
5.     double  mu20, mu11, mu02, mu30, mu21, mu12, mu03; /* central moments */    
6.     double  inv_sqrt_m00; /* m00 != 0 ? 1/sqrt(m00) : 0 */    
7. }    
8. CvMoments;    

在cvContourMoments()函数中,只用到m00,m01,...,m03几个参数;以mu开头的参数在其他函数中使用.

 

在使用CvMoment结构的时候,我们可以使用以下的函数来方便地一个特定的矩:

[cpp]  

1. CVAPI(double)  cvGetSpatialMoment( CvMoments* moments, int x_order, int y_order );    

调用cvContoursMonments()函数会计算所有3阶的矩(m21和m12会被计算,但是m22不会被计算).

 

再论矩

刚刚描述的矩计算给出了一些轮廓的简单属性,可以用来比较两个轮廓.但是在很多实际使用中,刚才的计算方法得到的矩并不是做比较时的最好的参数.具体说来,经常会用到归一化的矩(因此,不同大小但是形状相同的物体会有相同的值).同样,刚才的小节中的简单的矩依赖于所选坐标系,这意味这物体旋转后就无法正确匹配.

提供了计算Hu不变矩[Hu62]以及其他归一化矩的函数.CvMoments结构可以用cvmoments或者cvContourMoments计算.并且,cvContourMoments现在只是cvMoments

的一个别名.

一个有用的小技巧是用cvDrawContour()描绘一幅轮廓的图像后,调用一个矩的函数处理该图像.使用无论轮廓填充与否,你都能用同一个函数处理.

以下是4个相关函数的定义:

 

[cpp]  

1. /* Calculates all spatial and central moments up to the 3rd order */    
2. CVAPI(void) cvMoments( const CvArr* arr, CvMoments* moments, int binary CV_DEFAULT(0));    

[cpp]  

1. CVAPI(double)  cvGetCentralMoment( CvMoments* moments, int x_order, int y_order );    

[cpp]  

1. CVAPI(double)  cvGetNormalizedCentralMoment(CvMoments* moments,int x_order, int y_order);    

[cpp]  

1. /* Calculates 7 Hu's invariants from precalculated spatial and central moments */    
2. CVAPI(void) cvGetHuMoments( CvMoments*  moments, CvHuMoments*  hu_moments );    

 

第一个函数除了使用的是图像(而不是轮廓)作为参数,其他方面和cvContoursMoments()函数相同,另外还增加了一个参数.增加的参数isBinary如果为CV_TRUE,cvMoments将把图像当作二值图像处理,所有的非0像素都当作1.当函数被调用的时候,所有的矩被计算(包含中心矩,请看下一段).除了x和y的值被归一化到以0为均值,中心距本质上跟刚才描述的矩一样.

 

归一化矩和中心矩也基本相同,除了每个矩都要除以m00的某个幂:

最后来介绍Hu矩,Hu矩是归一化中心距的线性组合.之所以这样做是为了能够获取代表图像某个特性的矩函数,这些矩函数对于某些变化如缩放,旋转和镜像映射(除了h1)具有不变性.Hu矩是从中心矩中计算得到,其计算公式如下所示:

参考图8-9和表8-1,我们可以直观地看到每个图像对应的7个Hu矩.通过观察可以发现,当阶数变高时,Hu矩一般会变小.对于这一点不必感到奇怪,因为根据定义,高阶Hu矩由多个归一化矩的高阶幂计算得到,而归一化矩都是小于1的,所以指数越大,计算所得的值越小.

需要特别注意的是"I",它对于180度旋转和镜面反射都是对称的,它的h3到h7矩都是0;而"O"具有同样的对称特性,所有的Hu矩都是非0的. 使用Hu矩进行匹配

[cpp]  

1. /* Compares two contours by matching their moments */    
2. CVAPI(double)  cvMatchShapes( const void* object1, const void* object2,    
3.                               int method, double parameter CV_DEFAULT(0));   

很自然,使用Hu矩我们想要比较两个物体并且判明他们是否相似.当然,可能有很多"相似"的定义.为了使比较过程变得简单,OpenCV的函数cvMatShapes()允许我们简单地提供两个物体,然后计算他们的矩并根据我们提供的标准进行比较.

 

这些物体可以是灰度图图像或者轮廓.如果你提供了图像,cvMatchShape()会在对比的进程之间为你计算矩.cvMatchShapes()使用的方法是表8-2中列出的三种中的一种.

 关于对比度量标准(metric)是如何被计算的,表8-2中的三个常量每个都用了不同的方法.这个度量标准最终决定了cvMatchShapes()的返回值.最后一个参数变量现在不能用,因此我们可以把它设成默认值0.

等级匹配

我们经常想要匹配两个轮廓,然后用一个相似度量来计算轮廓所有匹配部分.使用概况参数的方法(比如矩)是相当快的,但是他们能够表达的信息却不是很多.

为了找到一个更精确的相似度量度,首先考虑一下轮廓树的结构应该会有帮助.请注意,此外的轮廓树是用来表述一个特定形状(不是多个特定形状)内各部分的等级关系.

类似于cvFindContours()着怎样的函数放回多个轮廓,轮廓树(contout tree)并不会把这些等级关系搞混,事实上,他正是对于某个特定轮廓形状的登记描述.

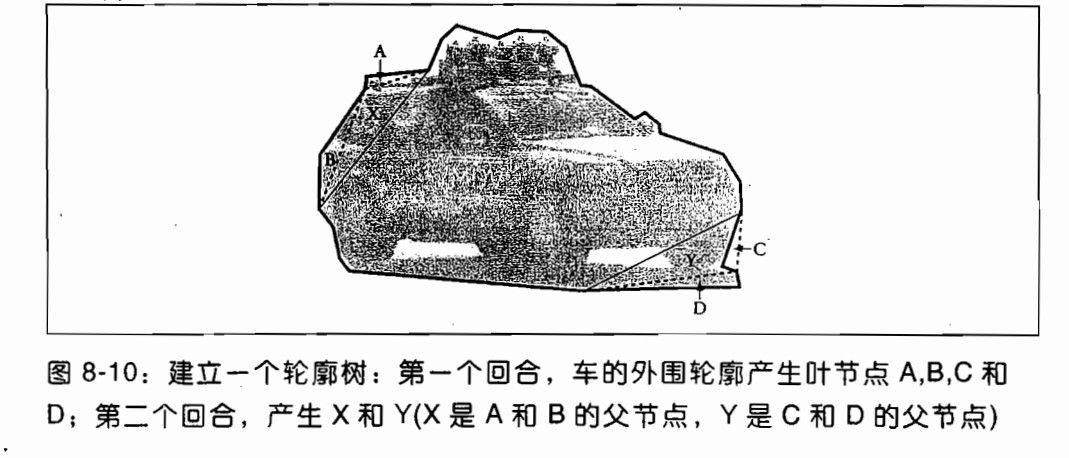
理解了轮廓树的创建会比较容易理解轮廓树.从一个轮廓创建一个轮廓树是从底端(叶节点)到顶端(根节点)的.首相搜索三角形突出或凹陷的形状的周边(轮廓上的每一个点都不是完全和它的相邻点共线的).每个这样的三角形被一条线段代替,这条线段通过连接非相邻点的两点得到;因此实际上三角形或者被削平(例如,图8-10的三角形D)或者被填满(三角形C).每个这样的替代把轮廓的顶点减少1,并且给轮廓创建一个新节点.如果这样一个三角形的两侧有原始的边,那么它就是得到的轮廓树的叶子;如果一侧是已存在三角形,那么他就是那个三角形的父节点.这个过程的迭代最终把物体的外形剪成一个四边形,这个四边形也被剖开;得到的两个三角形是根节点的两个子节点.

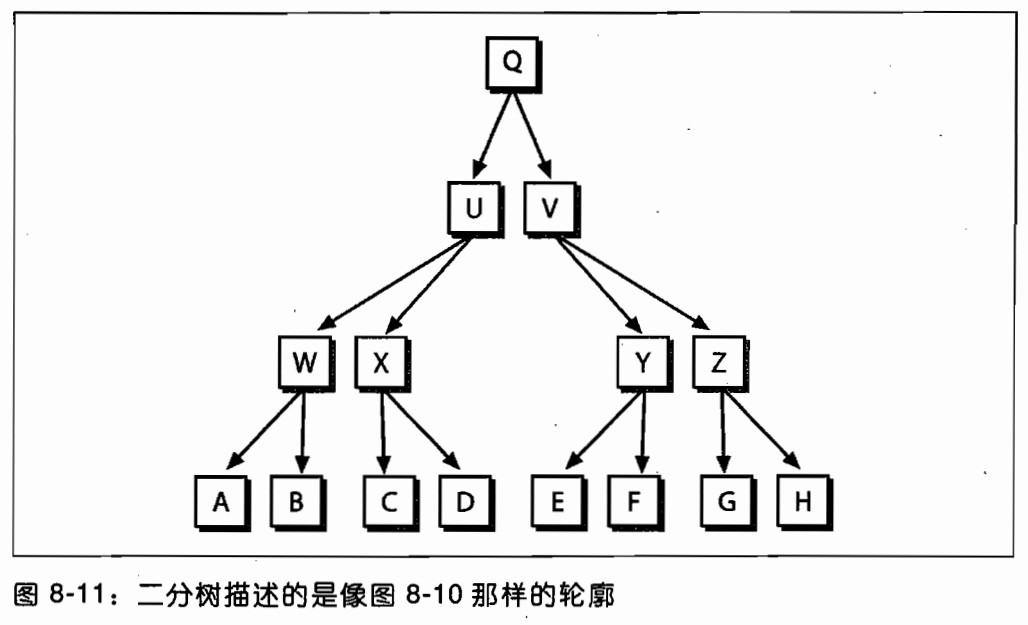
结果的二分树(图8-11)最终将原始轮廓的形状信息编码.每个节点被它对应的三角形信息(比如三角形的大小,它的生成是被切出来还是被填进去的,这样的信息)所注释

这些树一旦被建立,就可以很有效的对比两个轮廓.这个过程开始定义两个树节点的对应关系,然后比较对应节点的特性.对吼的结果就是两个树的相似度.

事实上,我们基本不需要理解这个过程.OpenCV提供了一个函数从普通的CvContour对象自动生成轮廓树并转换返回;还提供一个函数用来对比两个树.不幸的是,建立的轮廓树并不太鲁棒(例如,轮廓上很小的改变可能会彻底改变结果的树).同事,最初的三角形(树的根节点)是随意选取的.因此,为了得到较好的描述实现使用函数cvApproxPoly()之后将轮廓排列(运用循环移动)成最初的三角形不怎么受到旋转影响的状态.

CvContourTree* cvCreateContourTree(const CvSeq* contour,CvMemStorage* storage,double  threshold);

CvSeq * cvContourFromContourTree(const CvContourTree* tree,CvMemStorage* storage, CvTermCriteria  criteris);

double cvMatchContourTrees(const CvContourTree* tree1,const CvContourTree* tree2,int method,double threshold);

这个代码提到了CvTremCriteria(),该函数细节将在第9章给出.现在可以用下面的默认值使用cvTermCriteria()简单建立一个结构体.

CvTermCriteria termcrit = cvTermCriteria(CV_TERMCRIT_ITER | CV_TeRMCRT_EPS,5,1);

轮廓的凸包和凸缺陷

另一个理解物体形状或轮廓的有用的方法是计算一个物体的凸包(convex hull)然后计算其凸缺陷(convexity defects)[Homma85].很多复杂物体的特性能很好的被这种缺陷表现出来.

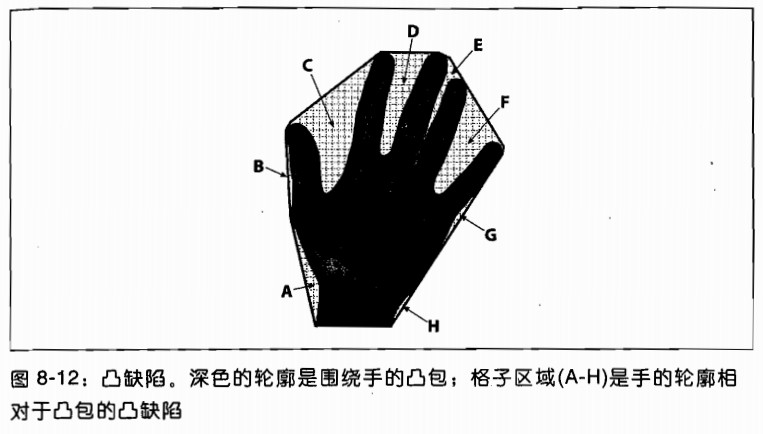
图8-12用人手举例说明了凸缺陷这一概念.手周围深色的线描画出了凸包,A到H被标出的区域是凸包的各个"缺陷".正如所看到的,这些凸度缺陷提供了手以及手状态的特征表现的方法.

 

[cpp]  

1. enum    
2. {    
3.     CV_CLOCKWISE         =1,    
4.     CV_COUNTER_CLOCKWISE =2    
5. };    

[cpp]  

1. /* Calculates exact convex hull of 2d point set */    
2. CVAPI(CvSeq*) cvConvexHull2( const CvArr* input,    
3.                              void* hull_storage CV_DEFAULT(NULL),    
4.                              int orientation CV_DEFAULT(CV_CLOCKWISE),    
5.                              int return_points CV_DEFAULT(0));    

[cpp]  

1. /* Checks whether the contour is convex or not (returns 1 if convex, 0 if not) */    
2. CVAPI(int)  cvCheckContourConvexity( const CvArr* contour );    

[cpp]  

1. /* Finds convexity defects for the contour */    
2. CVAPI(CvSeq*)  cvConvexityDefects( const CvArr* contour, const CvArr* convexhull,    
3.                                    CvMemStorage* storage CV_DEFAULT(NULL));    

 

 

OpenCV有三个关于凸包和凸缺陷的重要函数.第一个函数简单计算已知轮廓的凸包,第二个函数用来检查一个已知轮廓是否是凸的.第三个函数在已知轮廓是凸包的情况下计算凸缺陷.

函数cvConvexHull2()的第一个参数是点的数组,这个数组是一个n行2列的矩阵(n×2),或者是一个轮廓.如果是点矩阵,点应该是32位整型(CV_32SC1)或者是浮点型(CV_32F1).下一个参数是指向内存存储的一个指针,为结果分配内存空间.下一参数是CV_CLOCkWISE或者是CV_COUNTERCLOCkWISE中的一个.这参数决定了程序返回点的排列方向.最后一个参数returnPoints,可以是0或1.如果设置为1,点会被存储在返回数组中.如果设置为0,只有索引被存储在返回数组中.索引是传递给cvConvexHull2()的原始数组索引.

读着可能要问:"如果参数hull_storage是内存存储,为什么它的类型是void* 而不是CvMemSotrage* ?",这是因为很多时候作为凸包放回的点的形式,数组可能比序列更加有用.可虑到这一点,参数hull_storage的另一个可能性是传递一个指向矩阵的指针CvMat*. 这种情况下,矩阵应该是一维的且和输入点的个数相同.当cvConvexHull2()被调用的时候,它会修改矩阵头来指明当前的列数.

有时候,已知一个轮廓但并不知道它是否是凸的.这种情况下,我们可以调用函数cvCheckContourConvexity().这个简单快速,但是如果传递的轮廓自身有交叉的时候不会得到正确的结果.

第三个函数cvConvexityDefects(),计算凸缺陷返回一个缺陷的序列.为了完成这个任务,cvConvexityDefects()要求输入轮廓,凸包和内存空间,从这个内存空间来获得存放结果序列的内存.前两个参数是CvArr*,和传递给cvConvexHull2()的参数input的形式相同.

[cpp]  

1. typedef struct CvConvexityDefect    
2. {    
3.     CvPoint* start; /* point of the contour where the defect begins */    
4.     CvPoint* end; /* point of the contour where the defect ends */    
5.     CvPoint* depth_point; /* the farthest from the convex hull point within the defect */    
6.     float depth; /* distance between the farthest point and the convex hull */    
7. } CvConvexityDefect;    

函数cvConvexityDefects()返回一个CvConvexityDefect结构体的序列,其中包括一些简单的参数用来描述凸缺陷.start和end是凸包上的缺陷的起始点和终止点.depth_point是缺陷中的距离凸包的边(跟该缺陷有关的凸包便)最远的点.最后一个参数depth是最远点和包的边(edge)的距离.

 

 

成对几何直方图

Freeman链码编码是对一个多边形的的序列如何"移动"的描述,每个这样的移动有固定长度和特定的方向.但是,我们并没有更多说明为什么需要用到这种描述.

Freeman链码编码的用处很多,但最常见的一种值得深入了解一下,因为它支持了成对几何直方图(PGH)的基本思想.

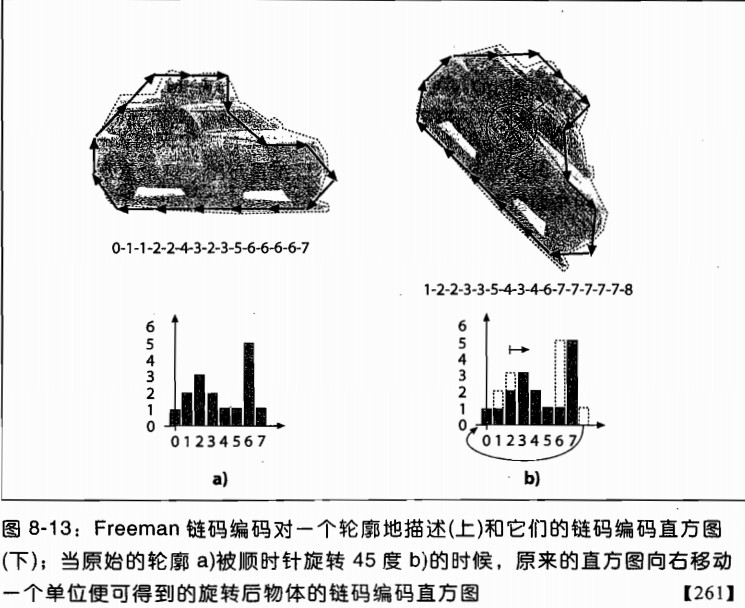
PGH实际上是链码编码直方图(CCH)的一个扩展或延伸.CCH是一种直方图,用来统计一个轮廓的Freeman链码编码每一种走法的数字.这种直方图有一些良好的性质.最显著的是,将物体旋转45度,那么新的直方图是老直方图的循环平移(图8-13).这就提供了一个不被此类旋转影响的形状识别方法.

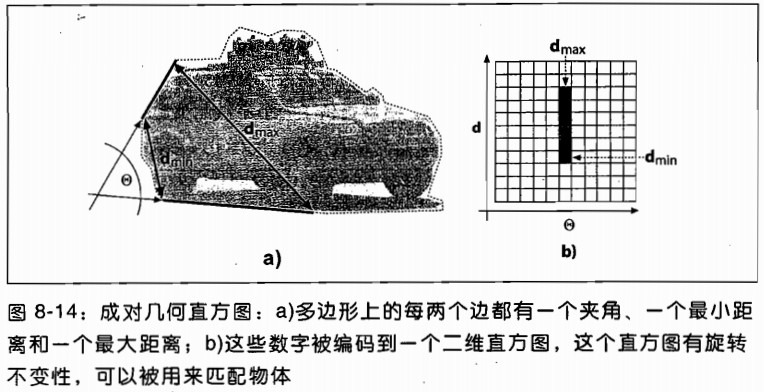
PGH的构成如下图所示(图8-14).多边形的每一个边被选择成为"基准边".之后考虑其他的边相对于这些基础边的关系,并且计算三个值:dmin,dmax和θ.dmin是两条边的最小距离,dmax是最大距离,θ是两边的夹角.PGH是一个二维直方图,其两个维度分别是角度和距离.对于每一对边,有两个bin,一个bin为(dmin,θ),另一个bin为(dmax,θ).对于这样的每一组边,这两个bin都被增长,中间值d(dmin和dmax之间的值)同样也被增长.

PGh的使用和FCC相似.一个重要不同是,PGH的描述能力更强,因此在尝试解决复杂问题的时候很有用,比如说大量形状需要被辨识,并且/或者有很多背景噪声的时候.用来计算PGh的函数是

void cvCalcPGH(const CvSeq* contour,CvHistogram* hist)

在这里轮廓可以包含整数值的点的坐标;当然直方图必须是二维的.